First, a picture for your viewing pleasure; you’ll need it:
[Baltimore inner harbour; rec area]
As a backlogged item, I was to give a little pointer to the design of control in (process-oriented!) industry, from which ‘we’ in the administrative world have taken some clues like sorcerer’s apprentices without due and proper translation and without taking the pitfalls of our botched translation job into account.
To start with, a little overview of the basics of how an industrial process (e.g., mixing paint, or medicine) is done, at the factory floor:
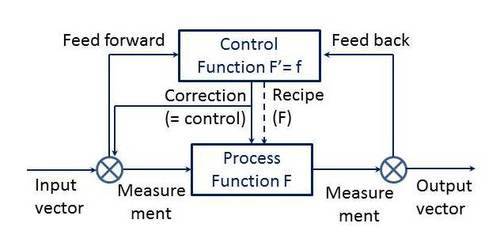
In which we see the main process as a (near- or complete) mathematical function of the input vector (i.e., multiple input categories) continuously (sic) resulting in the output vector which is supposed to come as close to a desired output as possible, continuously, on the parameters that matter. The parameters that matter, and the inputs, are measured by establishing values for parameters that we can actually measure, continuously (sic). With the inputs and outputs of course including secondary and tertiary ‘products’ like waste, heat, etc., and with all elements not being picture perfect but with varying variations off set values (the measuring devices and e.g. process hardware, also will have a fluctuating noise factor).
With the input vector being measured via the feedforward loop (control before anything might deviate) and the output vector being measured through the feedback loop (control by corrective actions, either tuning the process (recipe) or, more commonly, tuning the inputs). And the control function being the (near- or complete) mathematical derivative of the transformation function.
And all measurements being seen as signals; appropriately, as they concern continuous feeds of data.
That’s all, folks. There’s nothing more to it … Unless you consider the humongous number of inputs, outputs and fluctuations possible in all that can be measured – and not. In all elements, disturbances may occur, varying in time. So, you get the typical control room pictures from e.g., oil refineries and nuclear plants.
But there’s a bit more to it. On top of the control loop, secondary (‘tactical’, compared to the ‘operational’ level of which the simple picture speaks) control loop(s) may be stacked that e.g. may ‘decide’ which recipe to use for which desired output (think fuel grades at a refinery), and tertiary (‘strategic’ ..? Or would we reserve that for discrete whole new plants ..?). And there’s the gauges, meters and alarm lights in a dizzying array and display of the complexity of the main transformation function – the transformation function can be very complex! If pictured as a flow chart, it may easily have many tens if not hundreds of all sorts of (direct or time-delayed!) feedforward and feedback loops in itself. Now picture how the internals of that are displayed by measurement instruments…
Let’s put in another picture to freshen up your wiring a little:

[Baltimore, too; part of the business district]
Now then, we seem to have taken over the principles of these control designs into the administrative realm. Which may all be good, as it would be quite appropriate re-use of stuff that has proven to work quite soundly in the industrial process world with all its (physical, quality) risks.
But as latter-day newly trade trained practitioners, we seem to have not considered that there are some fundamental differences between the industrial process world and our bookkeeping world.
One striking difference is that the industrial process world governs continuous processes, with mostly linear (or understandable non-linear) transformation and control functions. Even in the industrial world, non-linearity but also non-continuous (i.e., discrete, in the mathematical sense) signals (sic) cause trouble, runaway processes and process deviations, etc.; these push the limits of the (continuous-, duh)control abilities.
Wouldn’t it be wise, then, if we had taken better care when making a weak shadow copy of the industrial control principles into the discrete administrative world …? Discrete, because even when masses of data points are available, they’re infinitely discrete as compared to continuous signals (that they sometimes were envisaged to represent)? Where was the cross-over from administering basic process / production data to administrating the derivative control measurements, and/or the switch from continous signals captured by sampling maybe (with reconstructability of the original signal being ensured by Shannon’s and other’s theories ..!!), to just discrete sampling without even an attempt to reconstruct(ability) of the original signals?
So we’re left with vastly un- or very sloppily controlled administrative ‘processes’, with major parts of ‘our’ processes being out of our scope of control (as is witnessed by the financial industry’s meltdown of 2007– ..!), non-linear, non-continuous, debilitatingly complex, erroneously governed/controlled (in fact, quod non) in haphazard fashion by all sorts of partial controller (groups) all with their own objectives, varying overwhelming lack of actual ‘process’ knowledge, etc.
Just sayin’. If you would have a usable (!) pointer to literature where the industrial control loop principles were carefully (sic) paradigm-transformed for use in administrative processes, I would be very grateful to hear from you.
And otherwise, I’d like to hear from you, too, for I fear it’ll be a silent time…
