Information Security – Page 47 – Maverisk / Étoiles du Nord

Is ID you?

[Guess the location]

Your digital ID becomes your pseudo-identity becomes who you are (considered to be), more than your actual you.
Your actual you, your innate identity, the one you discovered when only a couple of years old, will no longer be of interest to the world once your digital identity has all that the world cares about. Then, it can get stolen, lost, manipulated and altered, without you actually needing to notice. But who cares? Your digital ID is, you are just the carbon-based remnants of an outdated world. Just make sure there’s a fallback scenario that you can (or wouldn’t need to) prove you are you, your digital ID isn’t you.
The singularity may do away with you because you only use up scarce resource. You are not productive, your digital identity is. So you should care. Or?

If social media use ‘you’ as a resource, uses your apparent digital ID (ID and all posts, tweets, etc., turned into a persona, sold to all bidders) to operate, can you not deploy some artificial intelligence mechanism to do the socmed postings on your behalf ..? What’s the difference to the socmed companies that not your brain, but an artificial brain is used ..? Or do they already have their own farms of AI personas, to beef up traffic and sellable ‘user’ generated content ..?

Their AI personas may create a world separate from yours, a virtual world where they make money, not needing actual users anymore.
Your personal self may deploy AI to detach from their abusive, you-usurping world.
Case closed?

Why not Necker ..?

[Surprise in the (business) heart of Paris La Défense]

With all the hype about BYOD and the New Way of Working, flexible work place etc. having died down almost to zero, why are we still in offices ..? Why aren’t we all (…?) more like @richardbranson also for our working lives?
We certainly had the time to build a suitable infrastructure where there was none, if only under the guise (as it often is) of helping development (to the ideal level of material-only development that we have ..!?). I mean, cheap or free fast WiFi on any and all tropical beaches. Then, we could al have moved there and live a re-engineered happy life.

Oh, and we would have had to change the way we organise, and manage and control, work. Just a detail. The question seems to be: Why haven’t we?

Probably because of massive societal (level) fear of the Unknown. No, not fear of losing control, that’s just part, and one side, of it. We fear the loss of our warm, established social environment more than the gains of a warm, physically beneficial environment. Even if the gains are larger than the losses (that may be partial or replaced, in this case), fear drives more than hope (risk aversity).

Which may be overcome by the individual, by the minority that does venture out of the cave (see some earlier blog entry). But there, one might fear being the single odd one out, losing before gains could be had. Hm.
Or we could consciously take it step by step, starting with actual telework, videoconferencing etc. not immediately on a massive scale, just one by one (huh) or in small organisational communities. We need more of these dust grains in a supercritical fluid!
And at the same time, organise work better, bottom-up, in a sea of temporary collections of independent professionals banding together for a common goal (and with respective gains distributions) and then dissolving once the job’s done (project over, even if the project lasts decades like even blue chips are on average gone in half a century), to new ventures elsewhere.

Will we return (?) to a world where work is no longer life’s almost-single purpose but is maybe something bothersome just to earn the money to buy breathing space all the way down and up Maslow’s pyramid, and is something that caters to the higher levels of that so that all talent is expressed and rewarded ..? Looks like a ‘first world problem’ — hence one that can be solved!

Control, not privacy

In the discussions re privacy, there seems to be only two alternatives: Absolute privacy, with any individual holding complete, total and continuous control over who gets to see (not take in) any data point that may be, even in the remotest of ways, be recombined into anything useful for anyone – or Absolutely no privacy, everything being considered lost anyway and all one’s data being out there somewhere.

Which creates not some binary future state, but a bandwidth on which we should be able to choose. Because it is not privacy that people are concerned about, but the loss of control once data slips out of your hands. That is why everyone is so concerned when TLAs are found out to collect so much data on everyone (they have tried, and partially succeeeded, already for decades; nottoo many people were concerned) or when (not if) yet another credit card data processor looses some backup tapes. It is not the privacy in itself (one passes off the credit card number (and CVC) happily to just any unchecked device), it is not being able to get the data ‘back’, not being able to track the use in all the enormous amount of systems one knows is out there handling your data. Those systems ranging all the way from the benign to the crooked, always …

What we should have, then, is some mechanism by which we would be able to transparently and trasitively (sic) release the data we must (in order to get some service in return), and be rewarded for any data other parties earn money with (they are using your resource!), and not more. We’ll have control back; all we wanted.
Anything else, and we’ll end up in one of both extremes. To our own extreme detriment.

Inter faces

[Educational institute x 3, campus Free University, Amsterdam]

When sleeping over problems, one often comes up with solutions that both are real and so all-encompassing that they’ll need much elaboration before being applicable in a nimble way.
This one was/is on information security, again. Recall the ‘discussions’ I posted some days ago about (industrial) process control versus administrative control? Well, I’ve some more elements for a grand new scheme now.

It struck me that the operators at the (chemical) plant control room, are the ones with the dashboards. Not necessarily their managers. Nor their manager managers, etc. What if instead of some machine equipment, we plug in hoomans into the whole ..? And let them interact like the übercomplex ‘machines’ that they are, doing their (administrative / service) thing that they (want to?) do. All the way to the point where we have no equipment, just humans (with tools, by the way, but those would be under ‘complete’ control of the ones using them so are just extensions of them). One ‘manager’ could then control quite a lot; have a huge span of control…

If, big if, if only the manager would understand the overall ‘process’ well enough, that is, to be able to work with the dashboard then provided. Just Continuous Monitoring as a job, not much more (one would have 2nd- and/or 3rd ‘lines of control’ (ugh for the expression) to fix deviations, do planned maintenance, etc.). Probably not. But one can still dream; organizations would be flat without chaos breaking out.

And if you’d say it would be impossible altogether, have a look at your SOC/NOC room where techies monitor IT network traffic and systems’ health. They even have some room to correct..! And they are aware, monitor, the appropriateness of what flows over the lines, having professional pride in catching un(machine)detected patterns of irregularity possibly being break-in/break-out attempts. And they leave the content for what it is, that’s for the experts, the users themselves, to understand and monitor if only they would.
Why wouldn’t other ‘managers’ copy the idea to their own desk? No, they don’t, yet. They get Reports that they hardly read, because someone else had thought for them in determining what should be in there. And reports aren’t continuous. Walking around is, but would (rightly) be viewed as micromanagement and a bit too much given the non-continuous nature of what modern knowledge workers do. So, we’ll have to define some gauges that are monitored semi-continuously.

Now, a picture again to refresh:

[Westpunt, Curaçao]

But with the measurements not influencing the primary production ..! To let knowledge workers do their thing, in mutual cooperation without interference by some busybody thinking (s)he knows better for no reason whatsoever.
Through which we note that the use of dashboards should not, must not, start with ‘Board’s or similar utterly superfluous governance levels. Governance is for governments. As it is ‘implemented’ in larger organizations, it doesn’t look like kindergarten kids playing Important for nothing. The use of dashboards should start from the bottom, and should include quite rigorous (but not merely by the numbers) pruning of both middle-level ‘managers’ (keep the good ones, i.e., not the ones that are only expert in hanging on! otherwise you spell death), and all sorts of groupie secondary and third-line staff.

Which will only work if you haven’t yet driven out all the knowledge workers by dumbing down their work into ‘processes’ and ‘procedures’ that are bereft of any productive (sic) rationale. And if you haven’t driven out all the actual managers and are left with the deadwood that is expert only in toeing the line or rather, sitting dead still in their place.

Now have a look back also on how you do information security. Wouldn’t the little bit of tuning you may need to do, be focused best on the very shop floor level that go into the ‘industrial’ process as inputs? You would only have to informationsecure anything that would not be controlled ‘automatically’, innate in the humans that handle the information (and data; we’ll discuss later). Leave infosec mostly with them, with support concentrated at an infosec department maybe, and have managers monitor it only to the extent necessary.

And, by extension, the same would go for risk management altogether. Wouldn’t this deliver a much more lean and mean org structure than the top-down approaches that lead to such massive counterproductive overhead as we see today? With the very first-line staff that would need all the freedom feasible to be productive (the managers and rest of the overhead, aren’t, very very maybe only indirectly but certainly not worth their current income levels!) then not having to prove their innocence… See Menno Lanting’s blog for details…
Org structures have become more diamond- than pyramid-shaped; which is plain wrong for effectiveness and efficiency…

So let’s cut the cr.p and manage the interfaces, vertically, and horizontally, noting the faces part; human. An art maybe, but better than the current nonsense…

Predictions 2014; little update

[Paris La Defense; Metropolis-like]

Oh, a few notes to add to the Predictions 2014 blog:
Just saw that Smart, Cloud, Analytics and Mobile may abbreviate quite well… T not fitting in there…
Forrester (-‘16) rightly adds a rethink of ‘trust’ and ‘identity’
Gartner has ‘software defined everything’ and ‘3D printing’ in the mix. The former, Forrester has as well, when reading and recombining what they have (and G’s predictions may be regrouped as well, to form the F’s list, or the SCAM-T list).
Both don’t have Analytics, oddly enough. But via @duivestein, too, a good intro into Things.

Maybe we’d include Trust, Identity, Things abbreviated, before SCAM.
Back to predicting, I expect to see some hitherto unseen early signals re the dissolution of the absolute governance power of geography-bound countries / nation-states, and the nascence of (more) virtual communities with some form of barriers. Remember what I dropped as a note below on Bitcoin; I expect to see more of those in(ter)ventions. Interesting to see how the power balances (multiple) may play out: Will some developments be kidnapped / abused by states in a global (cold) cyberwar e.g., via or in the UN; how will the developments resist, and what will hold or not ..? This, too, may not be a thing for 2014 only (it may take decades!), but we’ll see some buds spring up next year.

That’s all. For now. Whether that’s Now, is another discussion entirely.

Predictions 2014

Already somewhere below, I noted that the Analytics part of SMAC(T) may need to be rephrased. Already now, I’m unsure whether to do that or just leave it unchanged. What I didn’t yet do, was to opine on the other elements so often put together.
First, a picture.

[Casa de Música Porto, for the chaotic structure of the future]

Now then:
Social everything: Yeah, yeah, of course there will be news. The decline of Fubbuck, etc. But will we see actual breakthrough hitherto unseen inventions of anything game-changingly new? I predict 2014 will be a pause year in which we’ll only see paradigm detailing and quite an improvement (sic) of the use of Social by medium- and larger sized enterprises. In somewhat innnovative ways, but nothing earth-shattering.

Mobile everything: The same, hopefully through the much-wanted huge improvements in cross-platform and cross-screensize compatibility and standardization. Which, too, would be refinement rather than absolutely unexpected New.

Analytics, we discussed, separately.

Cloud, ‘mehhh’ for theory, ‘hey how refreshing to be able to distinguish so clearly a good implementation’ in practice. Because that’s what we’ll see in 2014; cloud stuff deliberately done right. (Being deliberate, not by accident as it was in 2013!)

Things; The Internet Of ~, maybe, but in my view it’ll be too early. More like something for under the [Warning: European + derivative culture reference coming up] Christmas tree, to be played with in the year after.

Any other business?

Yes.

One with long odds: Clarity on the demise of “ERP” software. Of course, pre-2014 already the said administrative software, hardly ever used to its full potential but very often having been relegated into the bookkeeping role only, had been pushed away from the limelight into the back of the stage. But in 2014, we’ll see an acknowledgement of this, with consequences I cannot really predict very well – probably, all sorts of other software, more geared towards front-office functionality and integrating better architecturally with the bandwidth from there to the app/widget-world, will take over center stage.
[Update 2014 02 06: This link]

One with lesser odds: An enormous push for more information security, both at its operational, technical levels and upwards in renewal of structure (away from the stale, outdated ISO2700x sphere!) and inclusion of a more holistic approach (see some of my earlier posts, and probably some to come in the near future).
This will have a second leg in renewed interest in Business Continuity Management, not only by rule-based following of standards but also by more principle-based (sic) implementation of ISO 31000 (with all its drawbacks) throughout the business. If we can get our heads around the eradication of that ‘the business’ nonsense… and really integrate (continuity) risk-based management into general management, not needing too much 2nd or 3rd lines:

A final one: The deflation of TLD. The three lines don’t actually defend against anything but regulatory discovery of all that goes wrong in the business (from top to bottom and back again, there). As the previous prediction will already defend against actual mishaps, TLD will be shown to be emperor’s new clothes where lightning strikes. And oh will it strike; frappez, frappez toujours! it will and I hope. All those busybodies doing busywork, I just can’t stand it. The utter denouncement of humanity and human dignity …!

So, there you have it again; SMAC(T) weighed, and three more. Who make some interesting stuff available when I hit (or overshoot) five or more out of eight ..?

To close, another picture…

[Serralves, Porto – rainy outlook]

Control administration(s)

Before I forget: Some work has been done indeed on translating the industrial process (control) model to the administrative world. ACS’s KAD+ model (in Dutch) is an excellent example – especially the original KAD model at operational level that seems unsupported now. Maybe they are just a bit too far ahead of the curve, too clean-cut, to have found the traction they deserve.

That’s all, folks!
For now. Here’s a picture for your viewing pleasure:

[Alhambra, Granada]
Yeah, next up, some seriously long form blog again.

Control industry

First, a picture for your viewing pleasure; you’ll need it:

[Baltimore inner harbour; rec area]

As a backlogged item, I was to give a little pointer to the design of control in (process-oriented!) industry, from which ‘we’ in the administrative world have taken some clues like sorcerer’s apprentices without due and proper translation and without taking the pitfalls of our botched translation job into account.

To start with, a little overview of the basics of how an industrial process (e.g., mixing paint, or medicine) is done, at the factory floor:

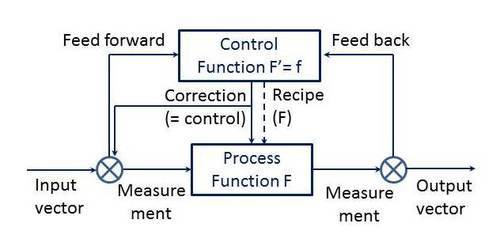
In which we see the main process as a (near- or complete) mathematical function of the input vector (i.e., multiple input categories) continuously (sic) resulting in the output vector which is supposed to come as close to a desired output as possible, continuously, on the parameters that matter. The parameters that matter, and the inputs, are measured by establishing values for parameters that we can actually measure, continuously (sic). With the inputs and outputs of course including secondary and tertiary ‘products’ like waste, heat, etc., and with all elements not being picture perfect but with varying variations off set values (the measuring devices and e.g. process hardware, also will have a fluctuating noise factor).
With the input vector being measured via the feedforward loop (control before anything might deviate) and the output vector being measured through the feedback loop (control by corrective actions, either tuning the process (recipe) or, more commonly, tuning the inputs). And the control function being the (near- or complete) mathematical derivative of the transformation function.
And all measurements being seen as signals; appropriately, as they concern continuous feeds of data.

That’s all, folks. There’s nothing more to it … Unless you consider the humongous number of inputs, outputs and fluctuations possible in all that can be measured – and not. In all elements, disturbances may occur, varying in time. So, you get the typical control room pictures from e.g., oil refineries and nuclear plants.
But there’s a bit more to it. On top of the control loop, secondary (‘tactical’, compared to the ‘operational’ level of which the simple picture speaks) control loop(s) may be stacked that e.g. may ‘decide’ which recipe to use for which desired output (think fuel grades at a refinery), and tertiary (‘strategic’ ..? Or would we reserve that for discrete whole new plants ..?). And there’s the gauges, meters and alarm lights in a dizzying array and display of the complexity of the main transformation function – the transformation function can be very complex! If pictured as a flow chart, it may easily have many tens if not hundreds of all sorts of (direct or time-delayed!) feedforward and feedback loops in itself. Now picture how the internals of that are displayed by measurement instruments…

Let’s put in another picture to freshen up your wiring a little:

[Baltimore, too; part of the business district]

Now then, we seem to have taken over the principles of these control designs into the administrative realm. Which may all be good, as it would be quite appropriate re-use of stuff that has proven to work quite soundly in the industrial process world with all its (physical, quality) risks.
But as latter-day newly trade trained practitioners, we seem to have not considered that there are some fundamental differences between the industrial process world and our bookkeeping world.

One striking difference is that the industrial process world governs continuous processes, with mostly linear (or understandable non-linear) transformation and control functions. Even in the industrial world, non-linearity but also non-continuous (i.e., discrete, in the mathematical sense) signals (sic) cause trouble, runaway processes and process deviations, etc.; these push the limits of the (continuous-, duh)control abilities.
Wouldn’t it be wise, then, if we had taken better care when making a weak shadow copy of the industrial control principles into the discrete administrative world …? Discrete, because even when masses of data points are available, they’re infinitely discrete as compared to continuous signals (that they sometimes were envisaged to represent)? Where was the cross-over from administering basic process / production data to administrating the derivative control measurements, and/or the switch from continous signals captured by sampling maybe (with reconstructability of the original signal being ensured by Shannon’s and other’s theories ..!!), to just discrete sampling without even an attempt to reconstruct(ability) of the original signals?

So we’re left with vastly un- or very sloppily controlled administrative ‘processes’, with major parts of ‘our’ processes being out of our scope of control (as is witnessed by the financial industry’s meltdown of 2007– ..!), non-linear, non-continuous, debilitatingly complex, erroneously governed/controlled (in fact, quod non) in haphazard fashion by all sorts of partial controller (groups) all with their own objectives, varying overwhelming lack of actual ‘process’ knowledge, etc.

Just sayin’. If you would have a usable (!) pointer to literature where the industrial control loop principles were carefully (sic) paradigm-transformed for use in administrative processes, I would be very grateful to hear from you.
And otherwise, I’d like to hear from you, too, for I fear it’ll be a silent time…

The P (part 1, too)

Now then, for the grand Part 1 of the People of Information Security. À la the triangle I posted on earlier (see somewhere below) where the People aspect floats around the triangle like a dense cloud; obscuring your clear view and posing a foggy unclarity threat.
To jot down, there are many aspects of People that we have to deal with, but let’s start with some random unstructured angles:
[Generalife, Granada]

People are a Threat. Externally, they are the actors, not random Acts of nature. No, they, they! the people, the masses (even in Ortega y Gasset style), they exist only to attack us!
How nice if you believe such, how nice to all those that have a sense of community and either don’t care to attack you even if it could be to their (risk-weighted) profit, or even help you, tacitly or visibly, explicitly. How hard do you work to alienate all those, too? Notwithstanding that there are indeed some out there that want to attack you: Have you ever stepped into their shoes to figure out why ..? If (very big if) you really stepped into their mindset, wouldn’t you do the same because by their reasoning, you ‘deserved’ it?

People are Vulnerabilities, on the inside. They are frail, failing their duty-above-all to follow your procedures, excuse me the word F.ck the contributions to the organizational success; your procedures are sacred of course?

People are Means in information security. That’s actually what they are in the People, Process, Technology trio. Vulnerability, and Threat by the way, if they deviate from how you wanted to deploy the resource, but they can also be very powerful ‘allies’ as resource to deploy in information security, information safety [nice idea, to defuse the old phrase], information asset protection. People are the thing (sic) that might follow Process using Technology to achieve protection. People are the ones to task doing to safeguard your information assets. They may not be perfect, but they will for a long time to come be the actual actors and re-actors.

People are psychological constructs acting in sociological environments. I cannot write this often enough: Read and re-read Bruce Schneier’s Liars and Outliers, to understand how these People may operate in your artificial society called organization (oh the wishful thinking in that word…).

People then, will have to be included in security design in the prominent role they have not as an afterthough. They will have to take center stage indeed, as alpha and omega of information security organization.
We’ll have to find ways to really start with People and see how their work may be structured, and how their work may be supported (not the other way around!!) by Process and Technology. Process as a little handy tool, not as the raison d’être – an uphill struggle it will indeed be, but also sign of the times already! Totalitarian bureaucrats beware; the Age of Compliance is waning. See a future blog. Technology as a little handy tool (in big plural), not as the first to arrive and to bolt a bit of Process and very maybe even People onto here and there.
But we haven’t explored such a design direction at all, yet! We have no clue, no metholodogy, no vocabulary, to describe such a ‘design’ …

That’s where you come in; through your comments I propose to crowdsource such a methodology. Be part of it!

No standards

[Looks like legend, but simply (?) is Segovia, Spain]
Hm, the title may read to some like this post would be about (finding) a temporary SO with low moral standards, but that wasn’t my intention.

For the more serious:
One should have standards, but have them for oneself. Imposing one’s standards on others, will not work. Self-dicipline trumps external discipline. The latter will compress the former, or make it explode through some hair crack into any unwanted direction(s). Because that former will always be present, in one way or another. Dormant, maybe, but there.

Hence standards must allow flexibility, or tie down to calcifying rigor that in the end will crumble into nothingness.
Because standards (try to) coerce subjects into conformity, standardization, uniformity, exactly-the-sameness. Death by lack of diversity. Because whatever is stamp pressed into a mold, will have to be something that must function in a variable, varying, diverse, diversifying, changed, changing environment. After the Information Explosion, ever more. To survive, diversity must be restored wherever possible. Compliance with simple standards will not cut it.

Standards must become compliant themselves, with flexibility requirements…